Bayes’ Theorem: Definition, Formula & Examples

---

KEY TAKEAWAYS

• Bayes’ Theorem is used to calculate the probability of an event occurring.
• It’s based on the fact that the probability of another event has already occurred.
• The Theorem comes from English statistician Thomas Bayes.
• Bayes’ Theorem can help make predictions based on past data.

---

What Is Bayes’ Theorem?

Bayes’ Theorem is a mathematical formula used to calculate the probability of an event occurring. It’s based on the fact that the probability of another event has already occurred.

There are several uses for this formula. And since you can update existing theories or predictions with it, Bayes’ Theorem proves quite useful.

Let’s explore the function of this formula to see exactly how it’s used. You will also find out how to calculate Bayes Theorem. And we have examples to further explain how it works.

History and Origin of Bayes’ Theorem

Bayes’ Theorem is named after English statistician Thomas Bayes (1701-1761). He first proposed it in an essay titled “An Essay towards solving a Problem in the Doctrine of Chances,” published posthumously in 1763.

French mathematician Pierre-Simon Laplace (1749-1827) often gets credit for formalizing the Theorem. He helped popularize it among mathematicians and statisticians.

In the centuries since Bayes and Laplace, others refined the Theorem. They’ve since applied it to a wide variety of problems in probability theory. For example:

• Statistics
• Machine learning
• Artificial intelligence
• Data mining
• Decision analysis
• And many other fields

Bayes’ Theorem is a cornerstone of the Bayesian approach to statistics, which many statisticians use today. Its application reaches many different avenues in the digital realm. Thus, it’s likely that we’ll be seeing even more of Bayes’ Theorem in the future.

In fact, this formula is presently going through a resurgence. You can find it in everything from the AI that dictates Google’s self-driving cars to cancer research. Bayesian proponents argue that everyone should use the theorem in everyday life decisions.

But opponents believe a line needs to be drawn somewhere. So while there’s debate regarding when to use the theorem, one area that it assuredly holds value is in the financial sector. Let’s explore this further in the sections below.

Where is Bayes’ Theorem Used?

Bayes’ theorem can calculate the probability that a borrower will default on a loan, given the borrower’s past credit history. For example, let’s say that a lender has two types of borrowers. One type has a good credit history, and the other type has a bad credit history. The lender can more easily make a decision as to whether to approve or deny the loan.

Bayes’ Theorem works in many other fields, as well. These include medicine, meteorology, artificial intelligence, and even law.

In medicine, Bayes’ Theorem calculates the probability that a person has a certain disease. This is according to the symptoms that the person is exhibiting.

For example, let’s say that a person comes into a doctor’s office with symptoms of the flu. The doctor knows that the probability of a person having the flu is 0.1 (or 10%).

However, the doctor also knows that these same symptoms could be caused by other illnesses. For example, they could result in a cold or allergies.

The doctor can use Bayes’ Theorem to calculate the probability that the person has the flu, given their symptoms. So as you can see, it’s quite useful in the medical field. Of course, its uses don’t stop there.

In meteorology, Bayes’ Theorem makes predictions about the weather. For example, a meteorologist may use data from past weather patterns to predict the likelihood of precipitation on a given day.

In artificial intelligence, Bayes’ Theorem works in machine learning. This is the process of teaching computers to make predictions based on data. For example, a computer might get data about houses in order to learn how to predict the sale price of a house.

Bayes’ Theorem can also work in law. For example, let’s say that a person is on trial for murder. The prosecutor knows that there is a 0.1% chance that any given person is a murderer (or 1 in 1000 people).

However, the prosecutor also knows that the victim died by a gunshot, and that only 0.01% of people own guns (or 1 in 10,000 people).

The prosecutor can use Bayes’ Theorem to calculate the probability that the person on trial is the murderer, given they owned a gun.

Bayes’ Theorem Formula

Bayes’ Theorem is typically written in the following form:

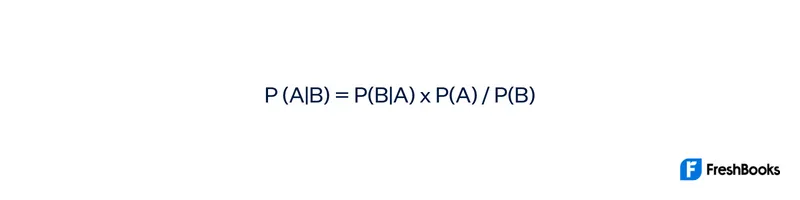
This may look intimidating at first, but it’s actually not too difficult to understand. Let’s break down each term in the formula:

Here:

P (A|B) is the probability that Event A will occur, given that Event B already occurred.

P (B|A) is the probability that Event B will occur, given that Event A already occurred.

P (A) is the probability that Event A will occur.

P (B) is the probability that Event B will occur.

Let’s look at each of these elements in more detail.

P (A|B) is the probability that Event A will occur, given that Event B already occurred. This is also known as the posterior probability.

P (B|A) is the probability that Event B will occur, given that Event A already occurred. This is also known as the likelihood.

 P (A) is the probability that Event A will occur. This is also known as the prior probability.

 P (B) is probability of Event B occurring. This is also known as the marginal likelihood or evidence.

If you need additional evidence, you can apply other models to your previous outcome. For now, these are exclusive outcomes for probability distributions.

 It’s worth noting that there are numerous forms of Bayes’ Theorem. There are simple forms, alternative forms, extended forms, and more.

 In its simple form, the formula looks like this:

 P(A|B) = P(B|A) x P(A)

 In its expanded form, the formula looks like this:

 P(A|B) = P(B|A) x P(A) / P(B)

 And in its alternative form, the formula looks like this:

 P(A|B) = P(A) x P(B|A) / P(B)

Now that we’ve looked at the history and motivation behind Bayes’ Theorem, let’s take a look at some examples of how you can apply it.

Suppose you’re a doctor and you want to know the probability that a patient has a certain disease, given the patient has a certain symptom.

You can use Bayes’ Theorem to calculate this probability.

First, you need to know the following:

The probability that a patient has the disease, regardless of whether or not they have the symptom. This is the prior probability.

The probability that a patient has the symptom, regardless of whether or not they have the disease. This is the likelihood.

The probability that a patient has the symptom, given they have the disease. This is the posterior probability.

You also need to know the base rate, which is the probability of the symptom occurring in the population.

Once you have all this data, you can plug it into Bayes’ Theorem. From there, you can calculate the probability that a patient has the disease, given the patient has the symptom.

Let’s explore a few more examples below to learn more.

Bayes’ Theorem Example

Let’s say that you’re trying to decide whether or not to buy a lottery ticket. You know that the probability of winning the lottery is 0.001 (or 1 in 1000). You also know that the probability of losing your money is 0.999 (or 999 in 1000).

Using Bayes’ Theorem, we may calculate the probability of winning the lottery, given that you bought a lottery ticket.

 P(win|ticket) = P(ticket|win) x P(win) / P(ticket)

 P(win|ticket) = 0.001 x 0.001 / 0.001

 P(win|ticket) = 0.001

This means that the probability of winning the lottery, given that you bought a lottery ticket, is 0.001 (or 1 in 1000).

Now let’s say that you’re trying to decide whether or not to buy a stock. You know that the probability of the stock going up is 0.5 (or 1 in 2). You also know that the probability of the stock going down is 0.5 (or 1 in 2).

Using Bayes’ Theorem, we may calculate the probability of stock prices going up, given that you bought it.

 P(up|stock) = P(stock|up) x P(up) / P(stock)

 P(up|stock) = 0.5 x 0.5 / 0.5

 P(up|stock) = 0.5

This means that the probability of the stock going up, given that you bought it, is 0.5 (or 1 in 2).

As you can see, Bayes’ Theorem can help you calculate the probability of an event occurring, given that another event has already occurred. 

Summary

Bayes’ Theorem is a powerful tool that can be used to solve problems in many different fields. This formula can be very helpful to lenders. By looking at a potential borrower’s lending history, lenders can determine whether a borrower is likely to repay their loan. 

A strong repayment history tells the lender that repayment to them is likely. Thus, Bayes’ Theorem can potentially save lenders time and money. 

It’s important to remember, however, that Bayes’ Theorem is only as good as the information plugged into it. If the information is inaccurate, then the results of the calculation will also be inaccurate.