Compound Probability: Definition, Formula & Examples

KEY TAKEAWAYS

• Compound probability is the occurrence of two independent events happening together, which are also known as compound events.
• Calculating compound probability is going to depend on the specific type of compound event. This, essentially, depends on whether or not the event is mutually exclusive or mutually inclusive.

What Is Compound Probability?

Compound probability relates to the occurrence of two independent events happening together. It’s a mathematical term, and it is equal to the probability of one event being multiplied by the probability of a second event. 

Insurance underwriters regularly use compound probability to help assess various risks when issuing premiums for certain insurance products. The concept of comp probability is widely used throughout the finance industry.

Compound Events and Compound Probability 

Within the core of probability theory, there are two main compound events. These are going to be mutually exclusive compound events and also mutually inclusive compound events. 

With mutually exclusive compound events, this means that two events can’t happen at the same time. Basically, if there are two events that are mutually exclusive, the probability of either of them happening ends up being the sum of their probabilities. 

Mutually inclusive compound events, on the other hand, are events that cannot happen without the other. So, if there are two events that are inclusive, the probability that either of them happening ends up being the total of their probabilities. But, it also considers subtracting the probability of both events happening. 

How Compound Probability Works

One of the most effective ways of understanding how compound probability works is the concept of flipping a coin twice. When you flip a coin once, you’re always going to have a 50 percent probability of it landing on tails. 

From here, the chances of the coin landing on tails twice in a row would be 25 percent. To calculate this, it would be (0.50 x 0.50) = .25

To consider compound probability, it always needs to combine at least two separate simple events, which is then known as a compound event. When you flip a coin only once, it means that one single flip is a single event. 

Now, when looking at compound probability in the case of insurance, it’s frequently used by underwriters to help determine and assess risk when issuing premiums for various insurance products. For example, an underwriter might want to know whether or not both members of a married couple will reach a certain age when it comes to health insurance or life insurance.

Or, for a different type of insurance premium, an underwriter might need to determine what the odds would be if two separate hurricanes hit at the same time in the same geographical region. Doing the calculations for compound probability helps them figure out an accurate amount to charge if you want to insure yourself or your property. 

 Formula of Compound Probability 

Calculating compound probability and the formula used will depend on whether or not the events are mutually exclusive or inclusive. It can also depend on independent probabilities, the probability activity, and probability distributions. 

For example, if there are two events that are mutually exclusive, the formula for probability would look like the following: 

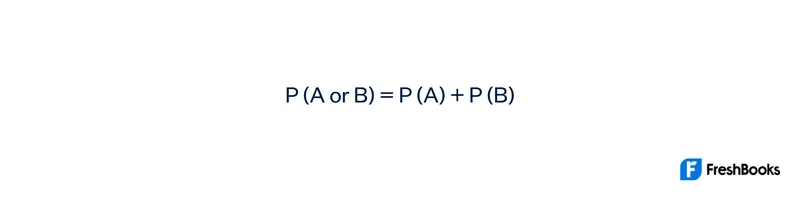
But, if there are two events that are mutually inclusive, the formula would look like this: 

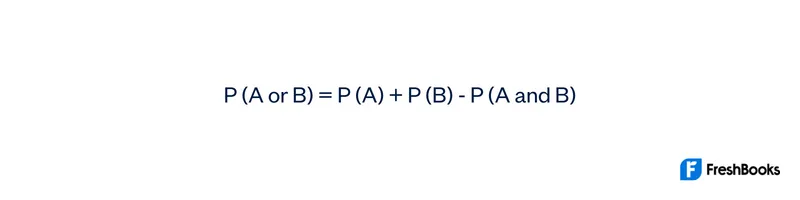
There are a few different methods that you could go about calculating compound probability, and the best way to describe it is to explain it in an example. 

One simple probability method is to use an organized list or a kind of tree diagram. This is where you would list each and every one of the potential outcomes that could end up happening. 

Example of Compound Probability 

Think about a coin flip or rolling a die. What would the probability be of the coin toss landing on tails and also rolling an even number on the die?

For this probability scenario, you would list the possible outcomes as Heads 1, Heads 2, and so on, in one column. In the next column, you would list Tails 1, Tails 2, and so on. Create a table with one event listed on the top row and the second event listed beneath it. 

After filling in the potential probabilities into the formula outlined above, you could calculate that there would be a 25 percent probability of flipping a coin on tails and also rolling an even number on the die. 

Summary 

The probability of compound events determines the likelihood of two or more events happening together. The events can either be mutually exclusive or mutually inclusive. Mutually exclusive events mean that two or more events can’t happen at the same time. 

To determine mutually exclusive events, the result of them happening is the sum of both probabilities. Mutually inclusive events, however, are separate events that cannot happen without each other. In this case, the sum of both probabilities happening is the result, but it also considers subtracting the possibility of both events occurring. 

Essentially, the compound probability is always going to end up between 0 and 1. It’s a widely used mathematical concept used throughout the finance and insurance industries. Underwriters, for example, would use the compound probability to assess potential risks and issue premiums for certain insurance policies.