Correlation Coefficient: Definition, Formula & Calculation

KEY TAKEAWAYS

• Correlation coefficient is a statistical metric that measures the relationship of two variables.
• A value of 0 means there is no relationship between two of the variables.
• A value of 1 means there is a strong positive relationship between two of the variables.
• A value of -1 means there is a strong negative relationship between two of the variables.
• Correlation coefficient is used in investing to identify relationships between stocks.

What Is the Correlation Coefficient?

Correlation coefficient measures a relationship of a pattern between variables. A value of 0 means that there isn’t a relationship between two of the variables. A value of 1 means that there is a strong positive relationship.

This means when one of the variables increases, the other also has a positive increase. And a value of -1 indicates strong negative relationships. This means when one of the variables increases, there’s a reduction in the other one. It’s important to understand this metric’s formula and calculation.

Correlation Coefficient Formula

A correlation coefficient is a measure that calculates how strong the relationship between two of the variables is. Here is the formula for correlation coefficient:

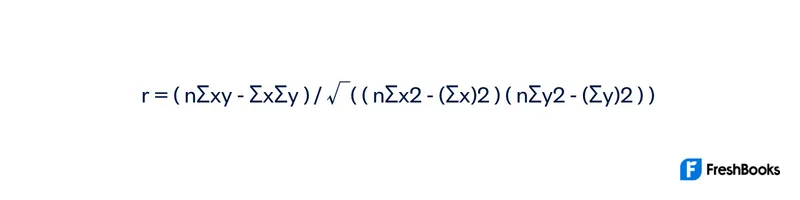
where:

r is correlation coefficient

n is the number of pairs of data points

Σxy is the sum of the products of the x-values and y-values

Σx is the sum of the x-values

Σy is the sum of the y-values

√((nΣx2 – (Σx)2)(nΣy2 – (Σy)2)) is the standard deviation of the x-values and y-values

Correlation coefficient equation measures the strength of the relationship between two of the variables. It can be anywhere from -1.0 to 1.0. A value of -1.0 means when one of the variables increases, there’s a decrease in the other one.

But a value of 1.0 means when one of the variables increases, there’s a positive increase in the other one, as well. A value of 0.0 means that there isn’t a relationship between two of the variables at all.

For the calculation of correlation coefficient, you will need a data set with at least two variables. The data can be in any format. But it is typically best to use something like a spreadsheet program so that you can easily input the data and calculate the results. This will help you see how closely related the two variables are.

After you have your data set, you need to find the mean, standard deviation, and sum of the variables. You can do this by hand or with a correlation coefficient calculator, but it is usually easiest to use a spreadsheet program. Once you have these values, put them into the formula above and solve for r.

Correlation Coefficient Calculation

Now that we’ve gone over the correlation coefficient formula, let’s take a look at how to calculate it. We’ll use the following data set for our example:

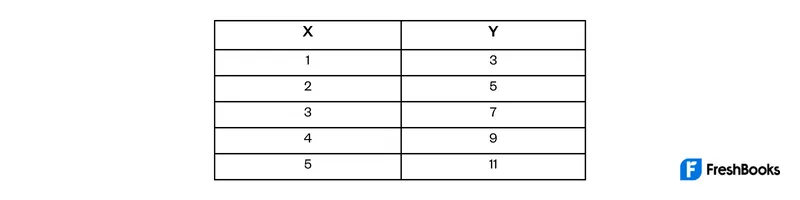
To calculate correlation coefficient equations, we first need to find a few things. These are the mean, standard deviation, and sum of each variable. Remember, you can do this by hand or with a calculator. But it is usually easiest to use a spreadsheet program. Once we have these values, we can plug them into the formula and solve for r.

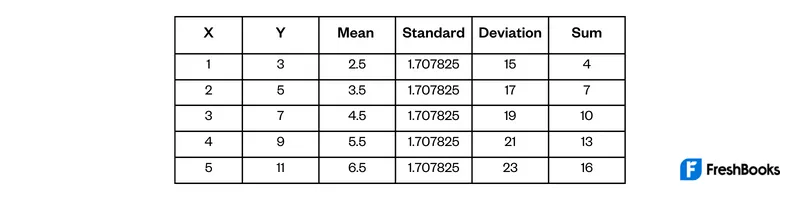
Now that we have all the necessary values, we can plug them into the formula and solve for r.

r = (5 * 15 – 2.5 * 23) / √((5 * 22.5 – 2.52)(5 * 30 – 6.52))

r = (-14.5) / √((-2.5)(-35))

r = (-14.5) / √(87.5)

r = -14.5 / 9.35

r ≈ -1.55

Correlation Coefficient in Investing

Correlation coefficient is used in investing to identify relationships between stocks. This can help investors diversify their portfolios and reduce market risk.

For example, let’s say you are considering adding two stocks to your portfolio. Stock A has a correlation coefficient of 0.8 with the stock market, while stock B has a correlation coefficient of -0.2 with the stock market. This means that stock A is more likely to move in the same direction as the stock market. Stock B is more likely to move in the opposite direction of the stock market.

You may want to consider adding both stocks to your portfolio composition. But you would probably weigh them differently. You would likely put more money into stock A than stock B because it is more likely to go up when the stock market goes up.

Correlation coefficients can also identify relationships between different asset classes. For example, stocks and bonds typically have a negative correlation coefficient. This means that when stocks are doing well, bonds are usually doing poorly, and vice versa.

This information can be useful for investors who are trying to diversify their portfolios. By investing in both stocks and bonds, they can offset some of the price risk associated with owning just one type of asset.

Correlation coefficient is just one tool that investors can use to make investment decisions. It is important to remember that there is no guarantee when it comes to investing. And even two assets with a high correlation can move in different directions at times.

Investors should always do their own research before making any investment decisions.

Limitations of Correlation Coefficient

The measure of correlation is a useful tool, but it does have some limitations.

First, correlation coefficient only measures linear relationships. This means that it can’t identify a nonlinear relationship. i.e., a linear relationship can’t identify a relationship between stock prices and company earnings.

Second, correlation analysis only measures the strength of the relationship, not the direction. This means that it can’t predict how one variable will move if the other variable moves.

For example, let’s say you want to know how stock prices will move if interest rates increase. Correlation coefficient shows how strong the relationship is between interest rates and stock prices. But it wouldn’t tell you which way stock prices will move.

Third, historical data is the basis for linear correlations. So it can’t predict future movements. The relationship between two of the variables can change over time. So just because they had a certain relationship in the past doesn’t mean they will have the same relationship in the future.

Fourth, correlation coefficient only measures the relationships between two of the variables. It can’t identify relationships between more than two variables.

For example, let’s say you want to know how stock prices will move if market interest rates increase and unemployment decreases. Correlation coefficients would not be able to help you answer this question. The reason is that it only measures the relationship between two of the variables.

Despite these limitations, correlation coefficient is still a useful tool for investors. It can help them understand the relationships between different asset classes. And it can help make investment decisions accordingly.

Correlation Coefficient Example

Let’s say you want to calculate the perfect correlation coefficient between stock A and the stock market. To do this, you would need to find some information. So let’s look at a sample correlation coefficient below and what you need.

• The return on stock A for each period
• The return on the stock market for each period
• The standard deviation of the return on stock A
• The standard deviation of the return on the stock market

You can find this information by looking at historical data or using a financial calculator. Once you have all of this information, you can plug it into the formula for correlation coefficient.

Correlation coefficient will tell you how closely stock A has moved with the stock market in the past. This information can be useful for making investment decisions.

Summary

The well-known correlation coefficient is a useful tool for investors. It offers insight into relationships between different asset classes. And it helps investors make investment decisions accordingly.

However, it is important to remember that correlation coefficient has some limitations. Investors should always do their own research before making any investment decisions.